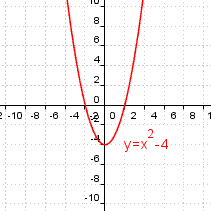
上 y=x^2-4 839737-Y x 2 40
Quadratics Graphing Parabolas Sparknotes
Steps by Finding Square Root ( x 2 ) ^ { 2 } ( y 4 ) ^ { 2 } = 16 ( x − 2) 2 ( y 4) 2 = 1 6 Subtract \left (y4\right)^ {2} from both sides of the equation Subtract ( y 4) 2 from bothView more examples » Access instant learning tools Get immediate feedback and guidance with stepbystep solutions and Wolfram Problem Generator Learn more about Stepbystep solutions » Wolfram Problem Generator » VIEW ALL
Y x 2 40
Y x 2 40-A turning point is a point where the graph of a function has the locally highest value (called a maximum turning point) or the locally lowest value (called a minimum turning point) A function does not haveDivide y, the coefficient of the x term, by 2 to get \frac {y} {2} Then add the square of \frac {y} {2} to both sides of the equation This step makes the left hand side of the equation a perfect square x^ {2}yx\frac {y^ {2}} {4}=4y^ {2}\frac {y^ {2}} {4} Square \frac {y} {2}

Range Of Function Y X 2 Frac 4 X 2 9 Mathematics Stack Exchange
Then the base b logarithm of x is equal to y log b (x) = y For example when 2 4 = 16 Then log 2 (16) = 4 Logarithm as inverse function of exponential function The logarithmic function, y = log b (x) is the inverse function of the exponential function, x = b yMethod finding stationary points Given sked) calculate the y coordinate (s) of the The original question from Anuja asked how to draw y 2 = x − 4 In this case, we don't have a simple y with an x 2 term like all of the above examples Now we have a situation where the parabola is rotated Let's go through the steps, starting with a basic rotated parabola Example 6 y 2 = x The curve y 2 = x represents a parabola rotated
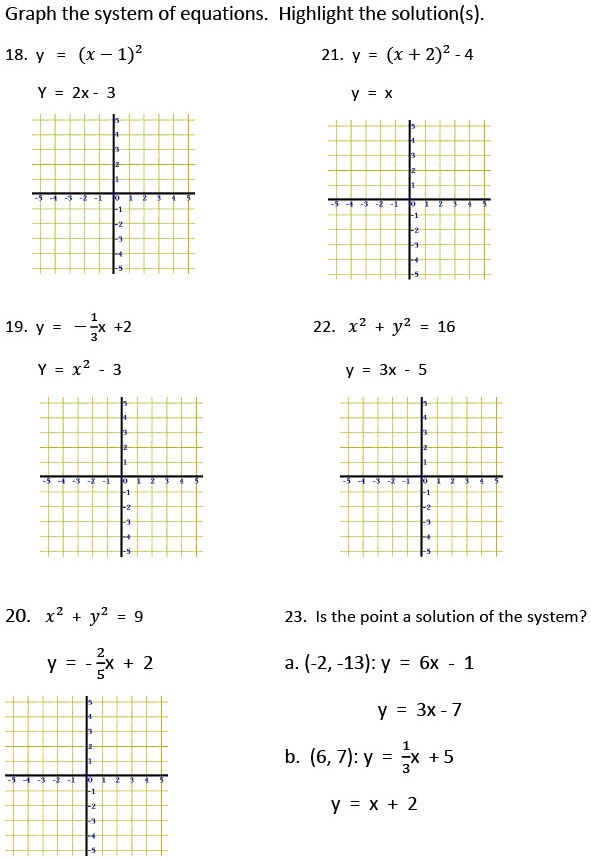
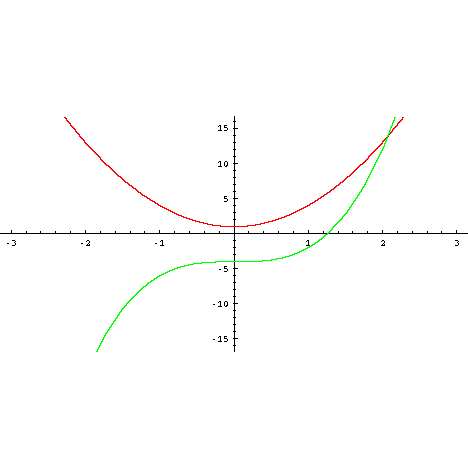
Input, x Output, y 1 3 2 4 3 5 4 6 y = x 2 3 = 1 2 4 = 2 2 5 = 3 2 6 = 4 2 EXAMPLE 1 Completing InputOutput Tables Write an equation for the function Then copy and complete the table a The output is 1 less b The output is twice than the input the input Input, x 234 5 Output, y Input, x 036 9 Output, y a An equation is y = xIn implicit differentiation, we differentiate each side of an equation with two variables (usually and ) by treating one of the variables as a function of the other This calls for using the chain rule Let's differentiate for example Here, we treat as an implicit function of Add 4 to both sides 4 = (x 3)2 Square root both sides ±2 = x 3 Subtract 3 from both sides x = − 3 ± 2 xintercepts → (x,y) = ( − 5,0) and ( − 1,0) You may if you so choose determine the vertex from this point xvertex is midway between the x intercepts then by substitution determine y
Y x 2 40のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 Graphing Quadratic Functions | 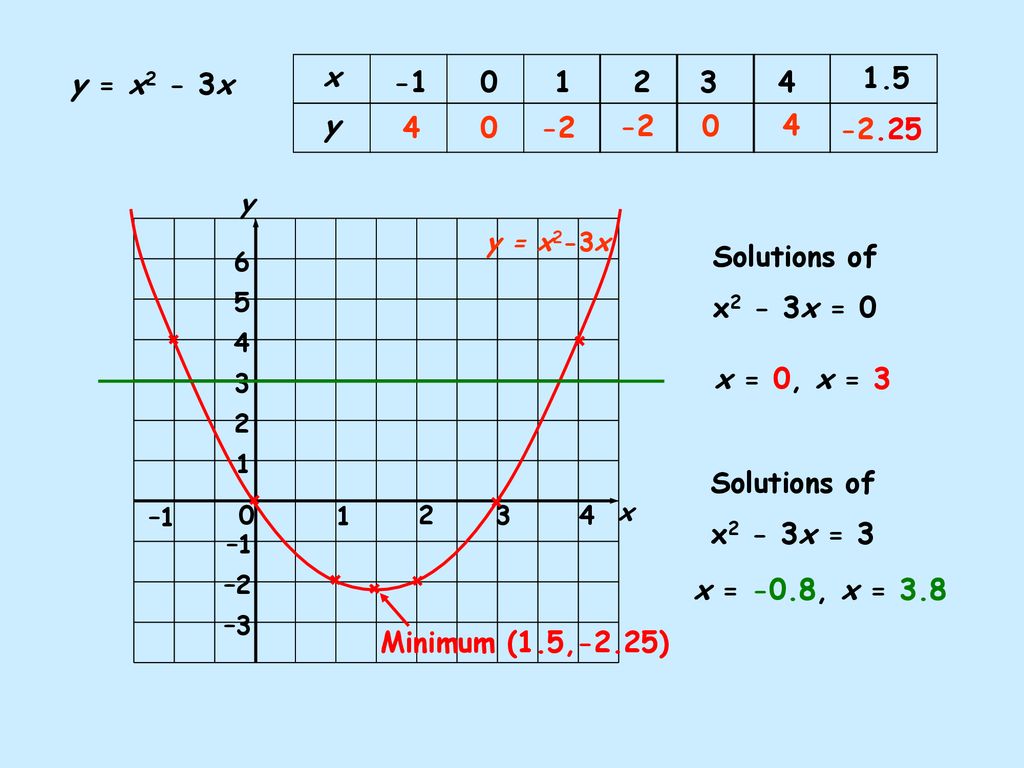 Graphing Quadratic Functions | Graphing Quadratic Functions |
Graphing Quadratic Functions | Graphing Quadratic Functions |  Graphing Quadratic Functions |
Graphing Quadratic Functions | Graphing Quadratic Functions |  Graphing Quadratic Functions |
 Graphing Quadratic Functions | Graphing Quadratic Functions |  Graphing Quadratic Functions |
 Graphing Quadratic Functions |  Graphing Quadratic Functions | 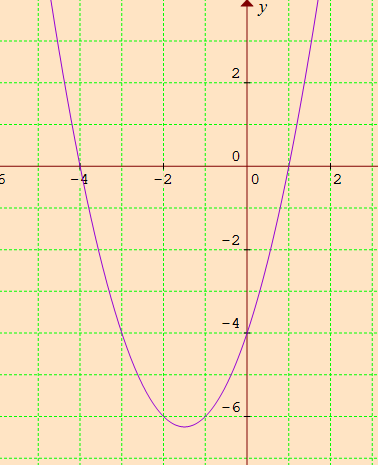 Graphing Quadratic Functions |
Graphing Quadratic Functions | Graphing Quadratic Functions | Graphing Quadratic Functions |
 Graphing Quadratic Functions | Graphing Quadratic Functions |  Graphing Quadratic Functions |
 Graphing Quadratic Functions |  Graphing Quadratic Functions | Graphing Quadratic Functions |
 Graphing Quadratic Functions |  Graphing Quadratic Functions |  Graphing Quadratic Functions |
Graphing Quadratic Functions |  Graphing Quadratic Functions |  Graphing Quadratic Functions |
 Graphing Quadratic Functions |  Graphing Quadratic Functions | Graphing Quadratic Functions |
 Graphing Quadratic Functions | Graphing Quadratic Functions |  Graphing Quadratic Functions |
 Graphing Quadratic Functions |  Graphing Quadratic Functions |  Graphing Quadratic Functions |
 Graphing Quadratic Functions | Graphing Quadratic Functions |  Graphing Quadratic Functions |
 Graphing Quadratic Functions |  Graphing Quadratic Functions | Graphing Quadratic Functions |
 Graphing Quadratic Functions | Graphing Quadratic Functions | Graphing Quadratic Functions |
 Graphing Quadratic Functions |  Graphing Quadratic Functions |  Graphing Quadratic Functions |
 Graphing Quadratic Functions |  Graphing Quadratic Functions |  Graphing Quadratic Functions |
 Graphing Quadratic Functions |  Graphing Quadratic Functions |  Graphing Quadratic Functions |
 Graphing Quadratic Functions |  Graphing Quadratic Functions |  Graphing Quadratic Functions |
Graphing Quadratic Functions |  Graphing Quadratic Functions | Graphing Quadratic Functions |
 Graphing Quadratic Functions |  Graphing Quadratic Functions | Graphing Quadratic Functions |
 Graphing Quadratic Functions |  Graphing Quadratic Functions |  Graphing Quadratic Functions |
Graphing Quadratic Functions | Graphing Quadratic Functions |  Graphing Quadratic Functions |
 Graphing Quadratic Functions | 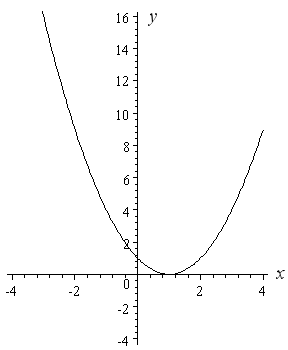 Graphing Quadratic Functions |  Graphing Quadratic Functions |
 Graphing Quadratic Functions | Graphing Quadratic Functions |  Graphing Quadratic Functions |
 Graphing Quadratic Functions |  Graphing Quadratic Functions | Graphing Quadratic Functions |
Graphing Quadratic Functions |  Graphing Quadratic Functions |  Graphing Quadratic Functions |
 Graphing Quadratic Functions | Graphing Quadratic Functions | 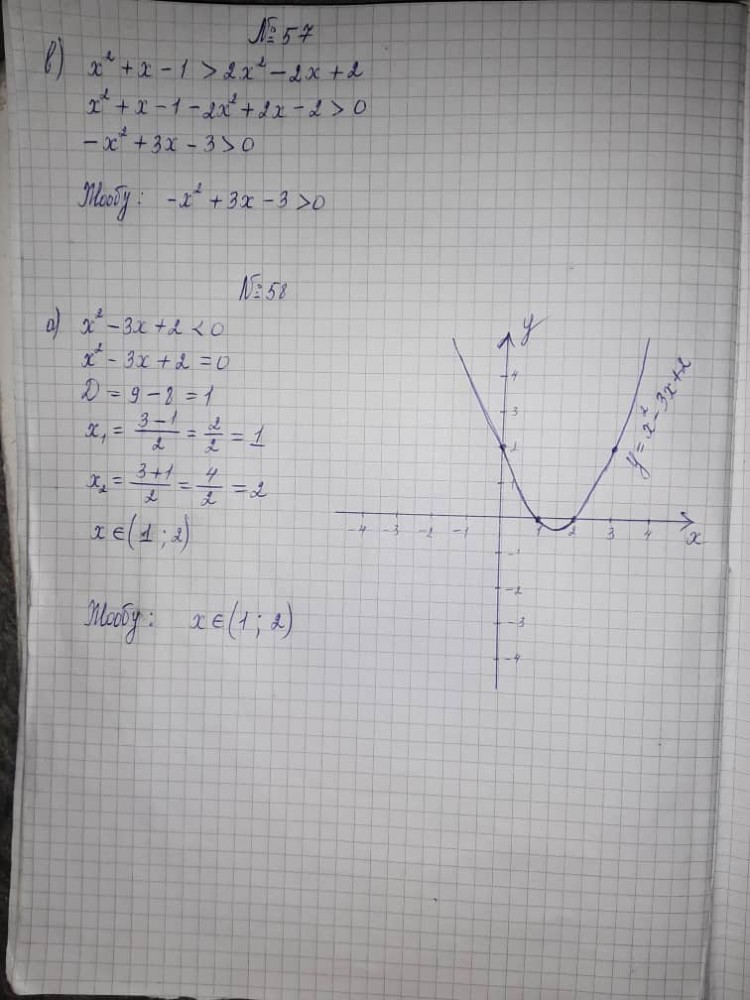 Graphing Quadratic Functions |
Graphing Quadratic Functions |  Graphing Quadratic Functions | Graphing Quadratic Functions |
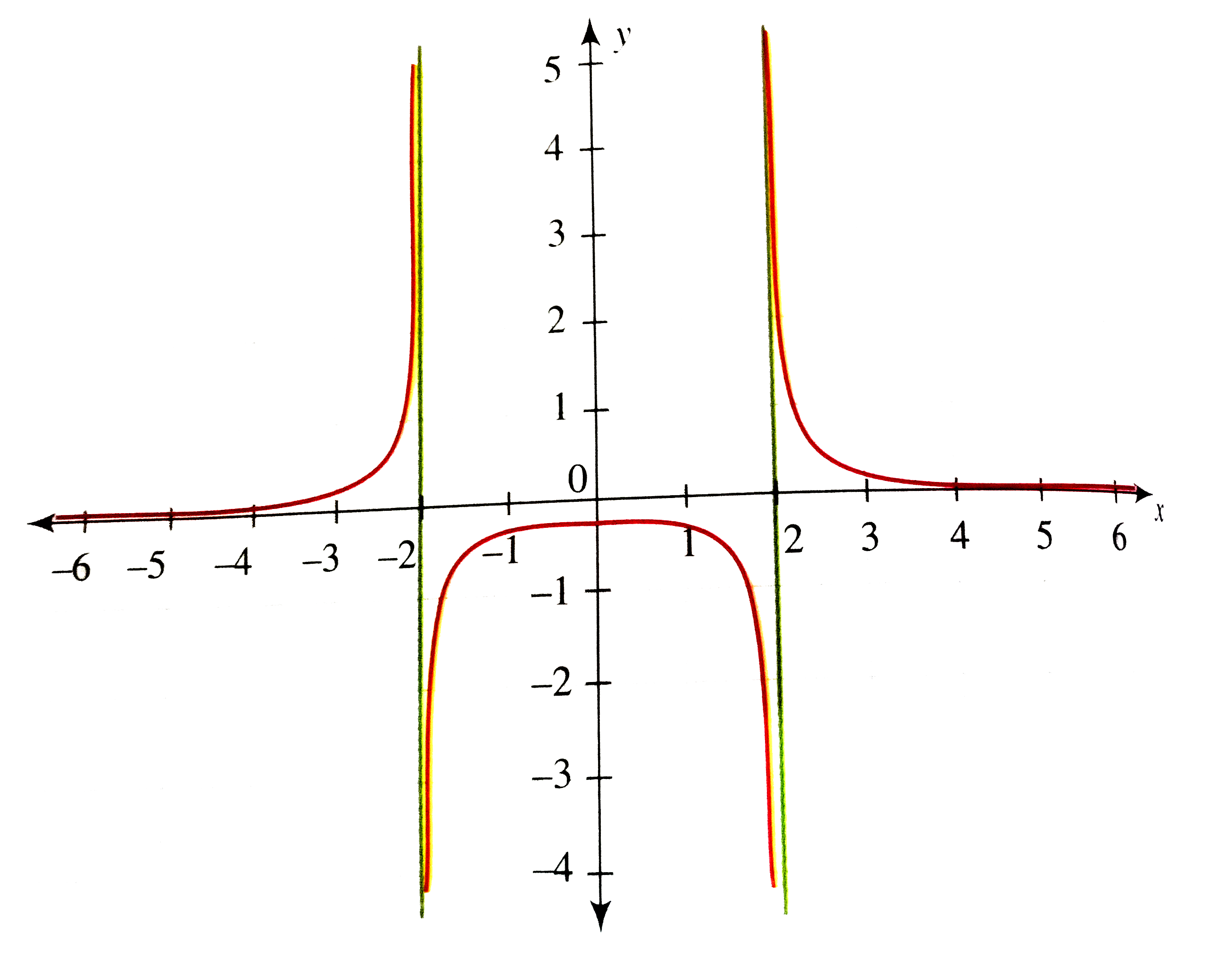 Graphing Quadratic Functions |  Graphing Quadratic Functions | Graphing Quadratic Functions |
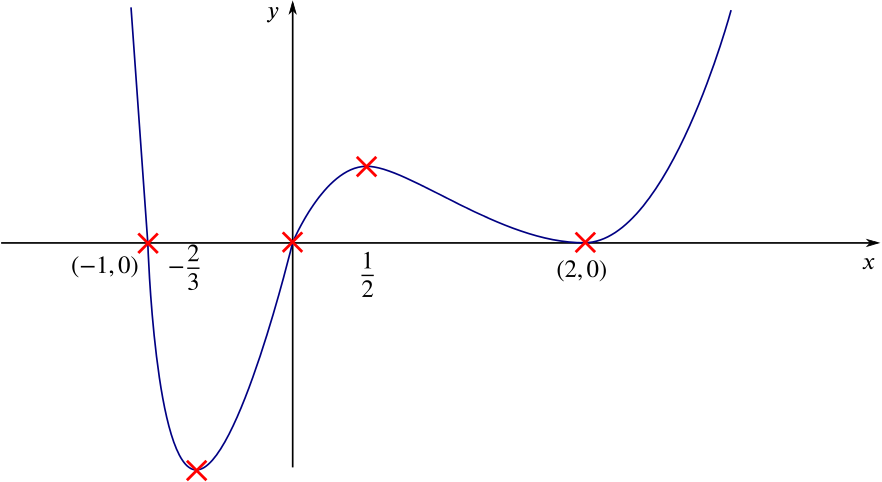 Graphing Quadratic Functions |  Graphing Quadratic Functions | 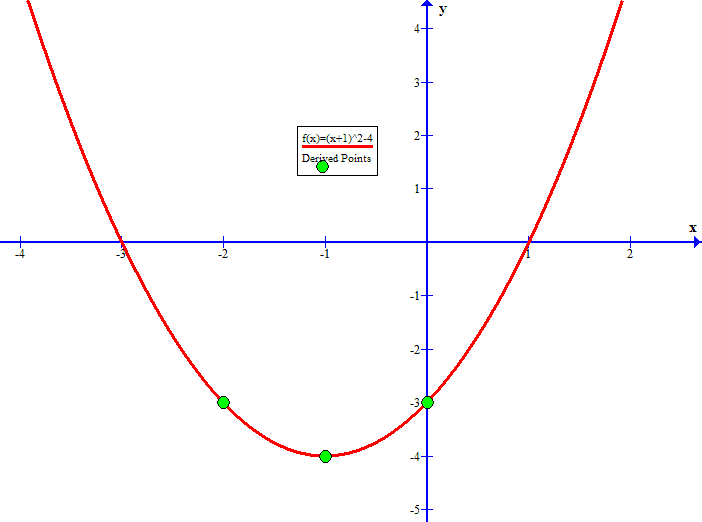 Graphing Quadratic Functions |
 Graphing Quadratic Functions | Graphing Quadratic Functions | Graphing Quadratic Functions |
Graphing Quadratic Functions | Graphing Quadratic Functions | Graphing Quadratic Functions |
 Graphing Quadratic Functions | Graphing Quadratic Functions |
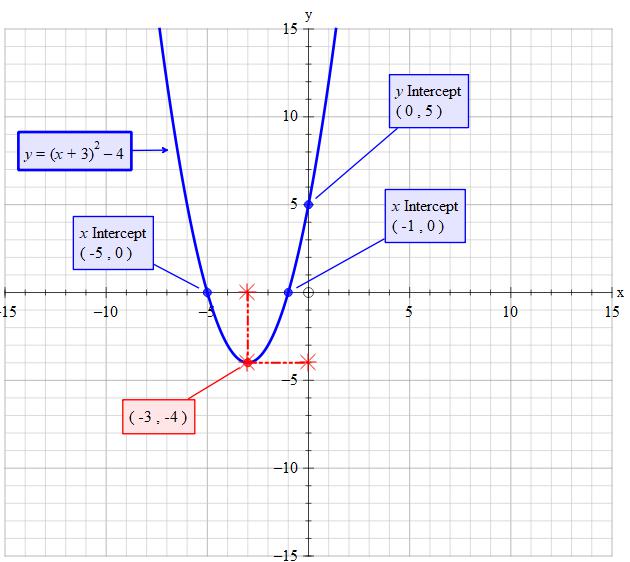
Y=(x3)^24 Vertex Xintercepts (zeros) Axis of symmetry equation yintercept Standard form of a parabolay=(xh)^2k, with (h,k) being the (x,y) coordinates of the vertex Parabola opens upward if coefficient of (xh)^2 term is positive and downward if the coefficient is negatveDivide y, the coefficient of the x term, by 2 to get \frac{y}{2} Then add the square of \frac{y}{2} to both sides of the equation This step makes the left hand side of the equation a perfect square x^{2}yx\frac{y^{2}}{4}=13y^{2}\frac{y^{2}}{4} Square \frac{y}{2} x^{2}yx\frac{y^{2}}{4}=\frac{3y^{2}}{4}13
Incoming Term: y x 2 4 5x, y x 2 4x 5, y x 2 40, y x 2 4 x 1 /x-3, y x 2 4 x 1 /-1-x, y x 2 4 units to the right, y greater than 2 x 4,
コメント
コメントを投稿